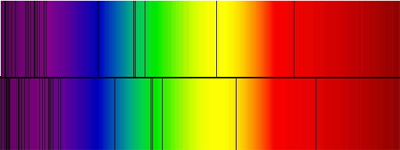
Lower spectrum sees absorption Lines shifted toward the red end.Astronomers calculate the distance of galaxies by using the Redshift characteristics of their spectra.
When a galaxy is receding it is found that there is a shift in the spectral absorption lines toward the red end of the spectrum.
The amount of shift is taken as the expected wavelength for a particular absorption line/band against the observed wavelength for the same band.
The spectrum at the top is what one expects to see and the one at bottom
is the observed spectrum. There is a noticable shift in the absorption
lines toward the red end of the spectrum.
A coefficient (z) is calculated for the amount of shift.
Lower spectrum sees absorption Lines shifted toward the red end.
z = observed wavelength - expected wavelength = V
expected wavelength C
where V is the recessional velocity and C the speed of light.
It is obvious from the above that the recessional velocity is Z times C:
V = ZC
Simply put; Z times the 'Hubble Age' of the universe [ ZH0 = D ] where D is the distance in millions of light years and H0 = 13.8 billion years.
While this formula is fine for objects moving at slower speeds we need to consider relativistic effects when the recessional velovity approaches the speed of light. For a more complete explanation see here.